ほえのブログ 
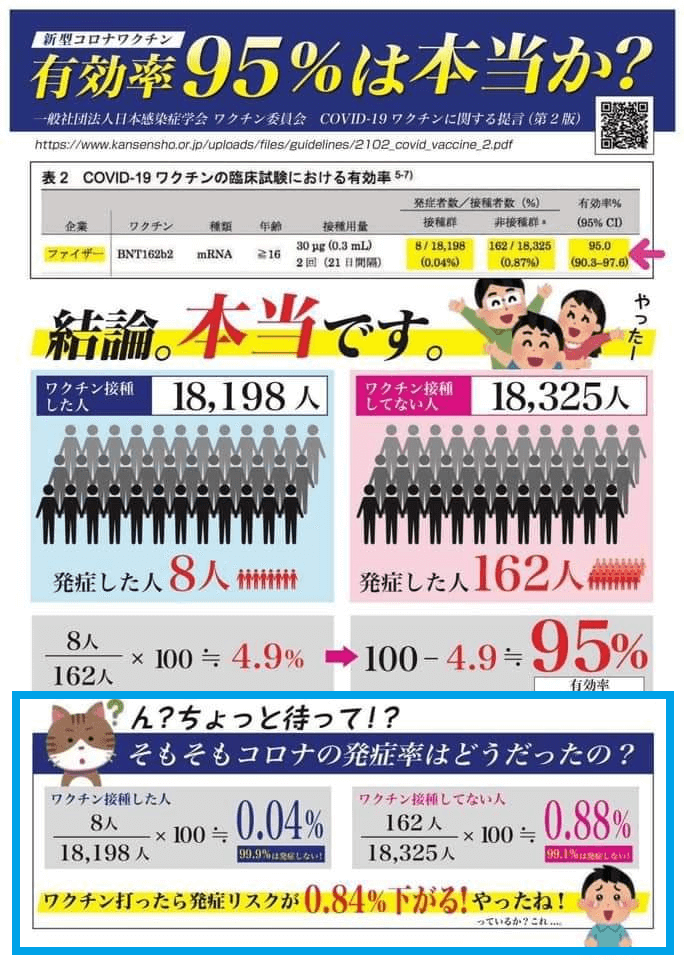
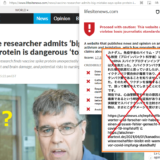
次のような画像を出して、「ワクチンを打った人と打たなかった人の発症リスクの差はたった０．８４％だ！ ワクチン打つ必要ないでしょ！」と主張する人がいますが、これは詐欺的理論によるごまかし（または非常に思慮不足）です。
問題は上図の下のほうの青枠の部分のところです。「ワクチン打ったら発症リスクが０．８４％下がる！やったね！」の下に小さい字で「っているか？これ…」と書いてあります。
そこに書かれている計算結果０．８４％は、「％の引き算の数値が小さいから実際の影響も小さい」と思わせるトリックです。
まぁ、ほぼ同じ母数（約１８，０００人）を対象とした調査で、
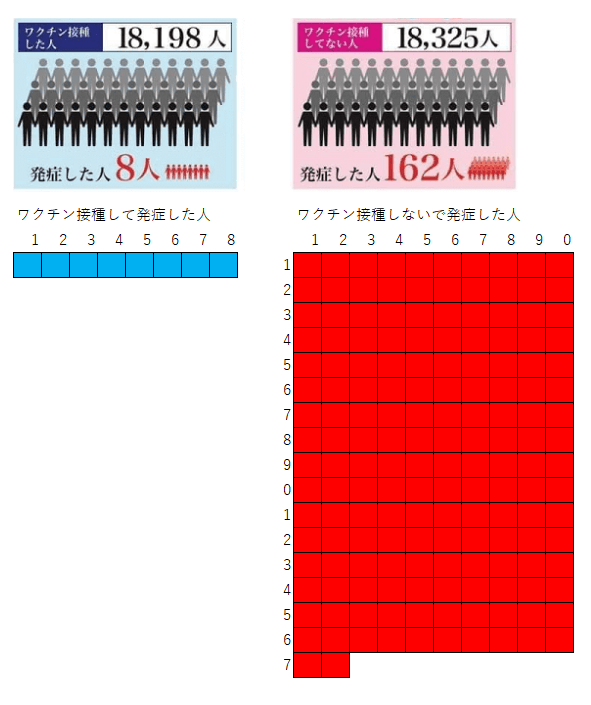
- ワクチン接種した人は８人が発症
- ワクチン接種してない人は１６２人が発症
というところで気付くと思いますが。
分かりやすく説明するために、計算する数値を変えて考えてみましょう。
たとえば、１から０．００１を引き算すれば、答えは０．９９９です。一般的な感覚からすると小さい数値のように感じます。
でも、１は０．００１の何倍ですか？
はい、１，０００倍ですね。引き算の数値自体は小さくても、２つの数値に大きな差があるのは明らかです。
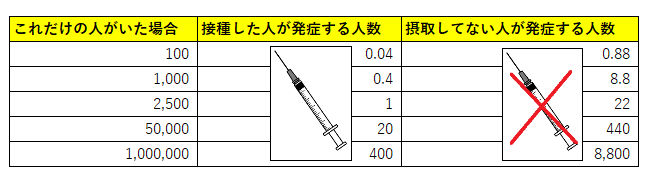
では上図の数値に戻って、発症率が「ワクチン接種した人０．０４％」「ワクチン接種してない人０．８８％」を実際の人数にあてはめて考えてみましょう。こうなります。
今回のケースでは、対象者（母数）約１８，０００人の中で接種してない人の発症が１６２人でしたが、感染の拡大が続く状況では、同じ母数の中で発症する人数も増えることを忘れてはいけません。
たとえば同じ母数１８，０００人の中で接種してない人の発症が１，６００人以上という状況もあり得るでしょう。
その場合、上の表の２列目と３列目の人数はそれぞれ１０倍になります。
これ見たほうが早いですかね？（笑）
１００万人の人がいた場合、ワクチンを接種すれば発症するのは４００人、接種しなければ８，８００人になる計算です。これは大きな違いですよね。２２倍の差があるということです。
今回の場合、対象者の母数が約１８，０００人の中で接種してない人の発症が１６２人でしたが、感染が蔓延してくれば、同じ母数の中でも発症する人数が増えることを忘れてはいけません。たとえば同じ１８，０００人の中で接種してない人の発症が１，８００人ということも有り得るでしょう。より少ない母数
しかも、感染症の感染というのは指数関数的に増えていく可能性があることを忘れないでください。１人が２人に感染させるとその２人が４人に、４人が８人に、というアレです。
指数関数的に増加するグラフ
最初のわずかな感染者数の違いでも、感染拡大時には大きな違いとなって増えていきますから、最初の２２倍の差というのはとてつもなく大きな意味を持っていると言えます。
デマッターのヘンテコ理論に騙されずに、元の生活を取り戻すために、ぜひ皆でワクチンを打ちましょう。
「ワクチンを打ったけれど発症した」という人と「ワクチンを打たずに発症した」という人を同じに考えてはいけないでしょう。
ワクチンを打った人は、発症したとしても、打たなかった人よりも症状が軽い可能性が高いわけです。症状が軽いということは、他人に感染させる確率も低くなると思われます。
こちらの漫画も同じ理由で誤解を招くものですね。
検索キーワード：
新型コロナワクチン 有効率９５％は本当か？ そもそもコロナの発症率はどうだったの ワクチン打ったら発症リスクが０．８４％下がる やったね！っているか？これ いえいえもっと凄いんですよ ９５％効くなんてすごいですよねぇ ９９．９％発症しなかったんですよ。そして９９．１％発症しなかった！ なんとその差１％以下 打った人と打ってない人の発症率の差です
